Lernaufgabe 8: Magnetische Kenntnisse anwenden
Hier findest du die Aufgaben ohne Lösungen.
Aufgabe 1
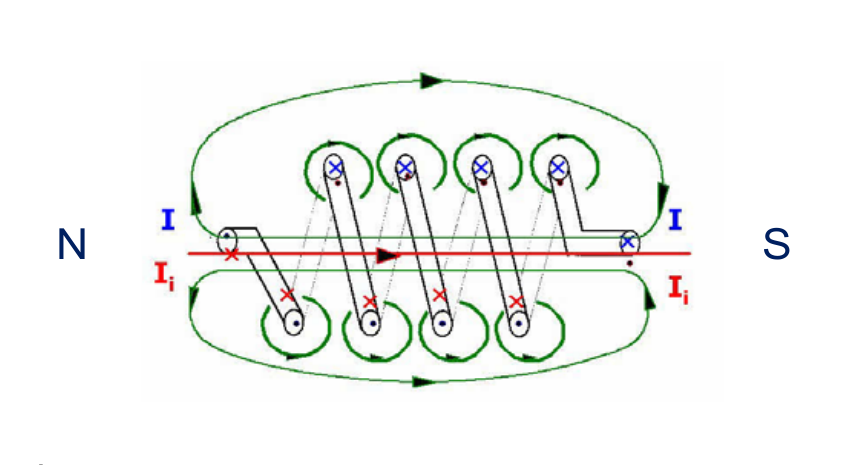
Zeichne den Verlauf der Feldlinien um die stromdurchflossene Spule und kennzeichne Nord- und Südpol.

Aufgabe 2
Eine Spule mit 300 Windungen und eine Spule mit 600 Windungen sollen die gleiche Durchflutung von \(\Theta=1200 A\) erzeugen.
Berechne die erforderlichen Stromstärken.
geg: \(N_1=300, N_2=600, \Theta=1200\ A\)
ges: \(I_1, I_2\)
Lös:
\(\Theta=I\cdot N\Leftrightarrow I=\frac{\Theta}{N}\)
\(I_1=\frac{\Theta}{N_1}=\frac{1200\ A}{300}=4\ A\)
\(I_2=\frac{\Theta}{N_2}=\frac{1200\ A}{600}=2\ A\)
Antw: Die Spule mit 300 Windungen benötigt einen Strom von \(4\ A\) und die Spule mit 600 Windungen einen Strom von \(2\ A\).
Aufgabe 3
In einer Spule mit 1500 Windungen soll ein Magnetfeld mit einer Flussdichte von \(B=12\ \frac{mVs}{cm^2}\) erzeugt werden. Durch die Spule fließt ein Wechselstrom von \(I=0,85\ A\) . Die Querschnittfläche der Spule beträt \(A=14cm^2\). Die Spule hat eine Länge von \(l=5\ cm.\)
Berechne die magnetische Durchflutung \(\Theta\), den Magnetfluss \(\Phi\) und die magnetische Feldstärke \(H\).
geg: \(N=1500, B=12\ \frac{mVs}{cm^2}, I=0,85\ A, l=5cm, A=14\ cm^2\)
ges: \(\Theta, \Phi, H\)
Lös:
\(\Theta=I\cdot N=0,85\ A\cdot 1500=1275\ A\)
\(B=\frac{\Phi}{A}\Leftrightarrow\Phi=B\cdot A=12\ \frac{mVs}{cm^2}\cdot 14\ cm^2= 168\ mVs\)
\(H=\frac{\Theta}{l}=\frac{1275\ A}{5\ cm}=\frac{1275\ A}{5\cdot10^{-2}\ m}=\frac{1275\cdot10^2\ A}{5\ m}=25500\frac{A}{m}=25,5\ \frac{kA}{m}\)
Antw: Die magnetische Durchflutung beträgt \(1275\ A\), der Magnetfluss \(168\ mVs\) und die magnetische Feldstärke \(25,5\ \frac{kA}{m}\).
Aufgabe 4
Gib an, wodurch im Bild a) und Bild b) Spannung in der Spule induziert wird.

In Bild a) durch Bewegung des Magneten und in Bild b) durch Bewegung der Spule.
Aufgabe 5
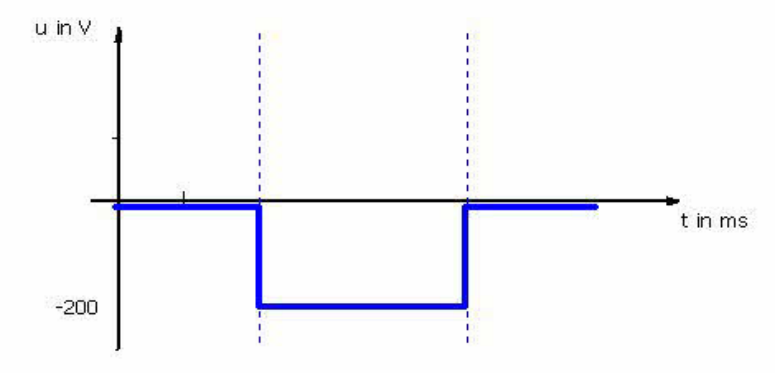
Der magnetische Fluss, der eine Spule mit 1000 Windungen durchsetzt, ändert sich gemäß der untenstehenden Abbildung.
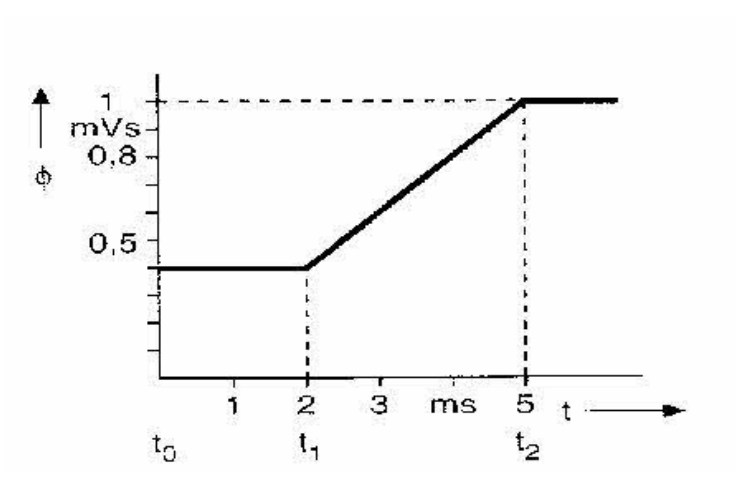
Ermittle aus dem Diagramm, wie groß die induzierte Spannung
1) zwischen den Zeitpunkten t0 und t1. \(\Rightarrow U_i=-N\cdot\frac{\Delta\Phi}{\Delta t}=-1000 \cdot\frac{0\ mVs}{2\ ms}=0V\)
2) zwischen den Zeitpunkten t1 und t2 \(\Rightarrow U_i=-1000\cdot\frac{0,6\ mVs}{3\ ms}=-200\ V\)
ist.
Zeichne das Zeitablaufdiagramm der Spannung \(U_i=f(t)\) unter das oben gezeigte Zeitablaufdiagramm des Magnetflusses \(\Phi =f(t)\).